Travel Tips
Lorem ipsum dolor sit amet, consectetur adipiscing elit.
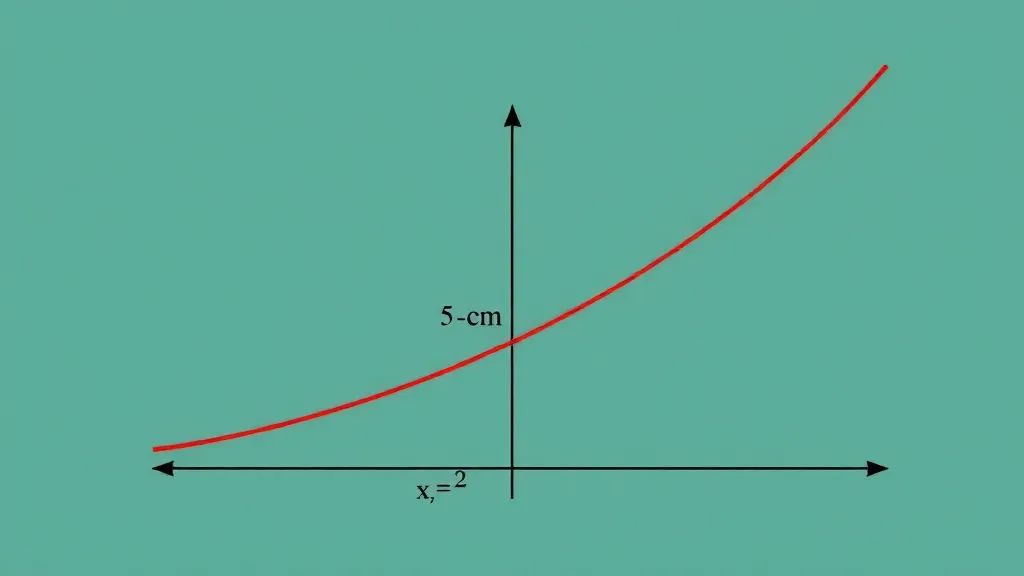
Desvendando a lógica por trás das funções exponenciais
As funções exponenciais são um dos conceitos mais fascinantes e importantes da matemática, com aplicações que vão desde a biologia até a economia. Uma função exponencial é uma função da forma f(x) = a * b^x, onde 'a' é uma constante, 'b' é a base da exponencial e 'x' é a variável. Para entender essas funções sem dificuldade, é essencial compreender suas propriedades e características.
Um dos aspectos mais importantes das funções exponenciais é o seu crescimento rápido. Quando a base 'b' é maior que 1, a função cresce rapidamente à medida que 'x' aumenta. Por exemplo, se considerarmos a função f(x) = 2^x, para valores de x como 1, 2 e 3, os resultados são 2, 4 e 8, respectivamente.
Isso ilustra como, mesmo um pequeno aumento em 'x', resulta em um aumento exponencial na função.
Além do crescimento, é crucial entender o conceito de decaimento exponencial. Quando a base 'b' está entre 0 e 1, a função descreve um decaimento.
Um exemplo clássico é a função f(x) = (1/2)^x, que representa a quantidade de uma substância que se reduz pela metade em intervalos de tempo regulares. Este conceito é amplamente utilizado em ciências naturais, como a física e a química, para descrever processos como a meia-vida de elementos radioativos.
As funções exponenciais também possuem uma característica única: a sua taxa de crescimento é proporcional ao seu valor atual.
Isso significa que quanto maior o valor da função, mais rápido ela cresce. Essa propriedade é frequentemente observada em fenômenos naturais, como a população de bactérias, onde a taxa de crescimento é proporcional ao número atual de bactérias.
Para facilitar o entendimento de funções exponenciais, é útil plotar gráficos.
O gráfico de uma função exponencial com base maior que 1 apresenta uma curva que sobe rapidamente, enquanto a curva de uma função com base entre 0 e 1 desce rapidamente. A visualização gráfica ajuda a compreender como as funções se comportam em diferentes intervalos de 'x'.
Outro ponto importante é a relação entre funções exponenciais e logaritmos.
O logaritmo é a operação inversa da exponenciação, e isso é fundamental para resolver equações envolvendo funções exponenciais. Por exemplo, se temos a equação 2^x = 8, podemos usar logaritmos para encontrar o valor de 'x', que neste caso é 3, já que 2^3 = 8.
A história das funções exponenciais remonta a séculos passados, com matemáticos como John Napier, que introduziu os logaritmos no início do século XVII.
Desde então, as funções exponenciais têm sido um tema central em várias áreas da matemática e ciências aplicadas, demonstrando sua relevância atemporal.
Por fim, para entender funções exponenciais sem dificuldade, é essencial praticar. Resolver problemas variados e aplicar os conceitos em diferentes contextos ajuda a solidificar o entendimento.
Livros de matemática, cursos online e plataformas educacionais oferecem uma vasta gama de recursos para quem deseja aprofundar seus conhecimentos sobre este tema fascinante.